
BatchDrake
Hacking, HAM Radio (EA1IYR), DSP, physics and more

Hacking, HAM Radio (EA1IYR), DSP, physics and more
In the previous post, we described the basic intuition behind demodulating frequency modulated NTSC. Suscan proved it was indeed possible, although a little bit of post-processing was necessary. In particular, the following issues were not properly addressed:
In this post, we will see how to fix these issues, top-down and in C. The resulting (hopefully small!) program will produce a bunch of PPM images containing the individual frames captured by my SDR receiver.
The signal is frequency-modulated, so in addition to the filtering step, we will need to perform an FM detection first. The resulting signal has to be level-adjusted to correctly map levels to brightness values. Later, we detect the horizontal sync pulses to align each line to the right, and last but no least, we detect the vertical synchronization pulse train to group lines into frames:

The program we are going to write to perform these operations will be as simple as possible: it will open the raw file with fopen(), read complex samples with fread() and process them in a simple while loop. Let’s name it ntsc.c, and its skeleton will look like this:
#include <stdio.h>
#include <stdlib.h>
#include <sigutils/sigutils.h>
#define INPUT_FILE "ntsc.raw"
#define SAMP_RATE 20e6
int
main(void)
{
FILE *fp;
SUSCOUNT samples = 0;
SUCOMPLEX x;
if ((fp = fopen(INPUT_FILE, "rb")) == NULL) {
fprintf(stderr, "error: cannot open %s\n", INPUT_FILE);
exit(EXIT_FAILURE);
}
while (fread(&x, sizeof(SUCOMPLEX), 1, fp) == 1) {
++samples;
}
printf(
"%d samples read (%g seconds of raw capture)\n",
samples,
samples / SAMP_RATE);
return 0;
}
The capture file (ntsc.raw) and the sample rate (20 Msps) were intentionally hardcoded. After compiling and installing sigutils, we can compile this program like this:
% gcc ntsc.c -o ntsc `pkg-config sigutils --cflags --libs` `pkg-config fftw3 --libs` `pkg-config sndfile --libs` -lm
The output will show the number of read samples and the total duration of the capture:
% ./ntsc
91946767 samples read (4.59734 seconds of raw capture)
Our program works because sigutil’s SUCOMPLEX is defined to match the format of gqrx’ I/Q sample. This is, 32 bit complex float (one float for the real part, another float for the imaginary part).
The centering and filtering step can be seen as the DSP equivalent of the tuning phase. The purpose of this block is to center in frequency the incoming signal (whose spectrum is shown below) and filter out all frequencies not belonging to the signal of interest.
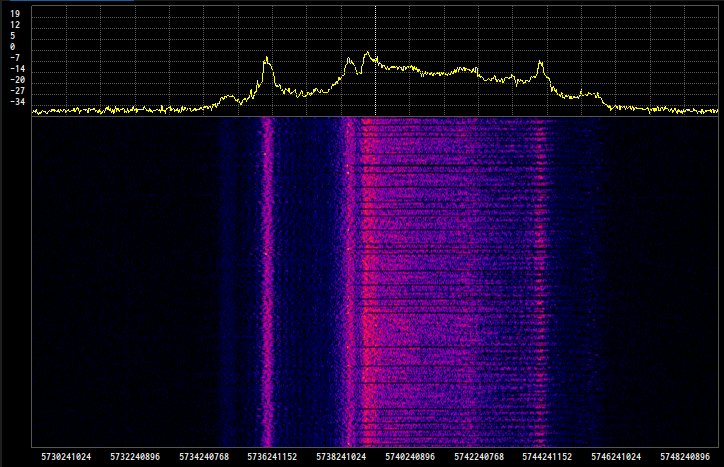
In FM, an appropriate choice of the center frequency is important as it affects the DC component in the demodulator’s output. It would be interesting for us to center the spectrum around the black level peak (which is 788 KHz below the capture frequency) to get values around zero for black and negative values for sync pulses after demodulation.
There’s another aspect to take into account: the spectrum around the black peak is not symmetric. If we rely on a simple low pass filter, we will be taking a lot of out-of-band noise that will affect the performance of our demodulator. There are two possible approaches here:
The first approach is slightly more convoluted because it requires two NCOs to perform the recentering. The second approach, although simpler in appearance, relies on a digital filter with complex taps. As of today, sigutils only supports FIR & IIR filters with real-valued taps (although this may change in the future). We will settle for the first approach for now.
Translation in frequency is equivalent to a product by a complex exponential in time. This is due to the convolution theorem of the Discrete Fourier Transform: the product of two signals in time domain is the convolution of both signals in frequency domain. Since the DFT of a complex exponential in time is just a Kronecker delta function in frequency, this operation boils down to a mere frequency translation:
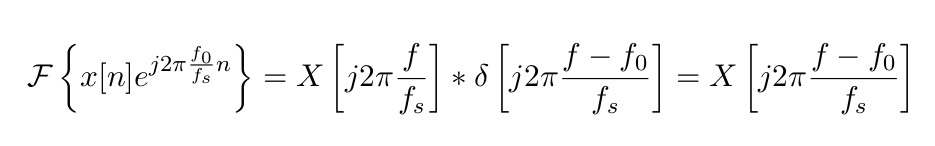
The tricky part comes when we want to put this into practice. We could naively multiply x in the code above by something like cexp(I * omega * samples). Unfortunately, this will not work in real life: as samples grows bigger and bigger, the rightmost bits in the significand of this product are progressively rounded off, losing precision and eventually distorting the shape of the resulting sinusoids.
What we need is a numerically-controled oscillator (NCO): a software object that samples a complex exponential of arbitrary frequency and length, capable of dealing with the aforementioned precision issues. This object is implemented in sigutils through the su_ncqo_t data type (defined in <sigutils/ncqo.h>).
A su_ncqo_t is initialized with a normalized frequency or, in other words, the number of half cycles per sample. For instance, if the su_ncqo_t was initialized with a normalized frequency of 0.1, it would take 20 samples to complete a cycle. Converting from absolute frequencies (the ones that take place in the real world) to normalized frequencies is rather straight forward, requiring only to know the sample rate. This conversion has been implemented in the sigutils macro SU_ABS2NORM_FREQ (defined in <sigutils/sampling.h>). The full code to initialize the NCO to the positive frequency of 788 KHz (because we want to move the spectrum 788 KHz to the right) would look like this:
su_ncqo_t nco;
su_ncqo_init(&nco, SU_ABS2NORM_FREQ(SAMP_RATE, 788e3));
Complex samples of this NCO can be iteratively retrieved simply by calling:
c = su_ncqo_read(&nco);
Now we have all the components to perform one of the most basic DSP operations: a simple frequency translation. In order to do this, we will open a second file for writing where we will output the raw samples of the transformed signal:
#include <stdio.h>
#include <stdlib.h>
#include <sigutils/sigutils.h>
#include <sigutils/sampling.h>
#include <sigutils/ncqo.h>
#define INPUT_FILE "ntsc.raw"
#define OUTPUT_FILE "demod.raw"
#define SAMP_RATE 20e6
#define FREQ_OFFSET 788e3 /* How far is the desired center frequency */
int
main(void)
{
FILE *fp, *ofp;
su_ncqo_t nco;
SUSCOUNT samples = 0;
SUCOMPLEX x, y;
if ((fp = fopen(INPUT_FILE, "rb")) == NULL) {
fprintf(stderr, "error: cannot open %s\n", INPUT_FILE);
exit(EXIT_FAILURE);
}
if ((ofp = fopen(OUTPUT_FILE, "wb")) == NULL) {
fprintf(stderr, "error: cannot open %s for writing\n", OUTPUT_FILE);
exit(EXIT_FAILURE);
}
su_ncqo_init(&nco, SU_ABS2NORM_FREQ(SAMP_RATE, FREQ_OFFSET));
while (fread(&x, sizeof(SUCOMPLEX), 1, fp) == 1) {
y = x * su_ncqo_read(&nco); /* Take sample from oscillator and mix */
fwrite(&y, sizeof(SUCOMPLEX), 1, ofp);
++samples;
}
printf(
"%d samples read (%g seconds of raw capture)\n",
samples,
samples / SAMP_RATE);
return 0;
}
I defined a couple of macros for the output filename and the desired offset frequency. The initialization of the NCO takes one line, and the frequency translation another line. Simple, right? :)
Note for the picky ones: I didn’t bother to close both files or to destroy the NCO on purpose. Obviously, we must take care of this in production code.
A way to test if our code works is to open the output file with Suscan as a raw I/Q file. Since we are neither interpolating nor discarding samples (decimating) the sample rate must remain the same. The resulting spectrum now looks like this:
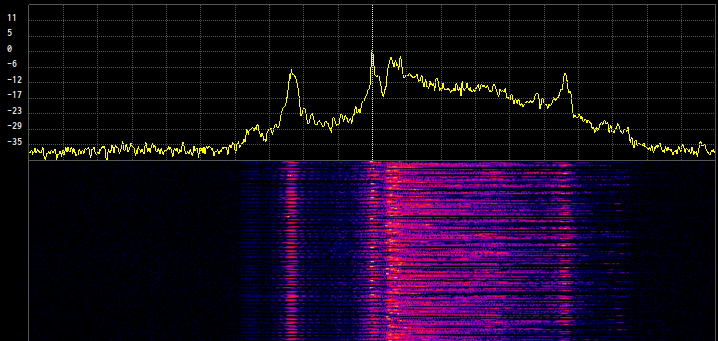
Note how the black level peak is now centered around DC. This is exactly what we have been looking for.
As we mentioned earlier, the spectrum of this signal is asymmetric and, due to restrictions in the sigutils filter API, we cannot perform arbitrary bandpass filtering. Therefore, we will need to re-center the spectrum again to its middle frequency, apply a low pass filter, and center it back to its the original frequency.
Computing these parameters with Suscan is rather easy. We just need to select the portion of the spectrum used by this video signal and open the channel menu to see its bandwidth and center frequency. We will do this directly on the processed output of the previous code:
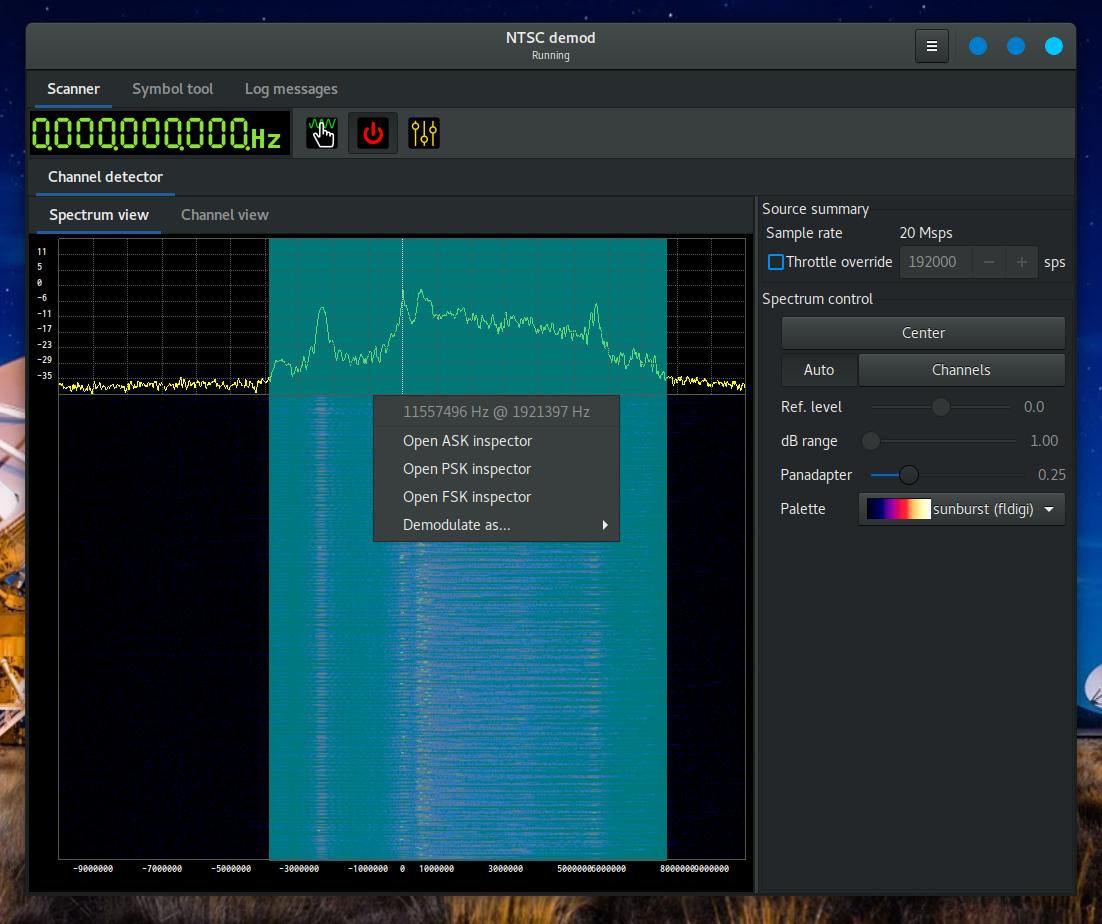
We see that the signal bandwidth is roughly 11.6 MHz, having its center at 1.91 MHz. Our strategy will be the following:
We will require two oscillators. The first one, tuned at -1.12 MHz, will center the spectrum to the middle frequency of the signal. The second one, tuned at 1.91 MHz, will center the spectrum around the black level peak again.
Regarding the filtering step, this is possible thanks to sigutil’s IIR/FIR filter API exposed in <sigutils/iir.h>. Sigutils also includes constructors for different digital Butterworth filters that can be used to perform the filtering we want. To initialize a low pass Butterworth filter of given bandwidth, we write:
su_iir_filt_t lpf;
if (!su_iir_bwlpf_init(&lpf, 5, SU_ABS2NORM_FREQ(SAMP_RATE, 11.6 / 2))) {
fprintf(stderr, "Cannnot allocate Butterworth lowpass filter\n");
exit(EXIT_FAILURE);
}
The initialization of a Butterworth filter allocates memory and therefore it may fail, so we should check the return value first. The number 5 refers to the order (i.e. number of taps) used by the filter. In general, the bigger the order, the narrower the transition band is. However, big orders also increase the chances of the filter to become numerically unstable (Butterworth filters are IIR filters after all). After some experimentation, I found that order 5 works for most real-world cases, but this says nothing about its numerical stability. Be warned!
Another important aspect to take into account is that this constuctor does not accept a bandwidth, but a cutoff frequency. For low pass filters, this is just the bandwidth divided by two.
Using this filter is also rather straight forward. An input sample is passed as second argument to su_iir_filt_feed while, at the same time, an output sample is returned by the function:
y = su_iir_filt_feed(&lpf, x);
Now we have all the ingredients to complete the filtering step in our program:
#include <stdio.h>
#include <stdlib.h>
#include <sigutils/sigutils.h>
#include <sigutils/sampling.h>
#include <sigutils/ncqo.h>
#include <sigutils/iir.h>
#define INPUT_FILE "ntsc.raw"
#define OUTPUT_FILE "demod.raw"
#define SAMP_RATE 20e6
#define FREQ_OFFSET 788e3 /* How far is the desired center frequency */
#define MID_FREQUENCY 1.91e6 /* Where is the spectrum center */
#define BANDWIDTH 11.6e6 /* Spectrum center */
int
main(void)
{
FILE *fp, *ofp;
su_ncqo_t nco1, nco2;
su_iir_filt_t lpf;
SUSCOUNT samples = 0;
SUCOMPLEX x, y;
if ((fp = fopen(INPUT_FILE, "rb")) == NULL) {
fprintf(stderr, "error: cannot open %s\n", INPUT_FILE);
exit(EXIT_FAILURE);
}
if ((ofp = fopen(OUTPUT_FILE, "wb")) == NULL) {
fprintf(stderr, "error: cannot open %s for writing\n", OUTPUT_FILE);
exit(EXIT_FAILURE);
}
su_ncqo_init(&nco1, SU_ABS2NORM_FREQ(SAMP_RATE, FREQ_OFFSET - MID_FREQUENCY));
su_ncqo_init(&nco2, SU_ABS2NORM_FREQ(SAMP_RATE, MID_FREQUENCY));
if (!su_iir_bwlpf_init(&lpf, 5, SU_ABS2NORM_FREQ(SAMP_RATE, BANDWIDTH) / 2)) {
fprintf(stderr, "error: cannot initialize lowpass filter\n");
exit(EXIT_FAILURE);
}
while (fread(&x, sizeof(SUCOMPLEX), 1, fp) == 1) {
y = x * su_ncqo_read(&nco1); /* Center spectrum */
y = su_iir_filt_feed(&lpf, y); /* Filter centered signal */
y = y * su_ncqo_read(&nco2); /* Center signal around the black level peak */
fwrite(&y, sizeof(SUCOMPLEX), 1, ofp);
++samples;
}
printf(
"%d samples read (%g seconds of raw capture)\n",
samples,
samples / SAMP_RATE);
return 0;
}
Now, the spectrum of the signal after processing looks like this:
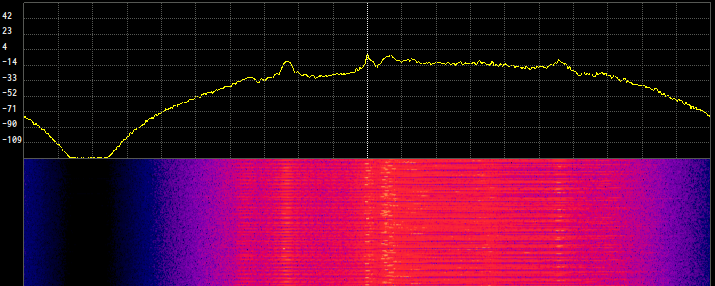
Which is roughly what we expected. The different peaks of the original signals have shrunk because of the relative magnitude of the attenuation of most out-of-band noise.
You may think that the attenuation is not that strong. Remember that this is still a logarithmic scale. Still, sigutils supports a more aggresive filtering technique (the spectral tuner, which performs frequency domain filtering) that I left uncovered again for the sake of simplicity.
Now we have a properly centered and filtered signal that is ready to be demodulated in the next block. In the next post, we will see the theory behind the quadrature demodulator, its properties and how it can be used to recover the instantaneous frequency of a complex exponential.
Stay tuned!