Automatic GRAVES monitoring with QStones
After some good feedback from my post about GRAVES and stonealert, I decided to invest some time on cleaning the code and providing a more handy user interface for the whole thing. Since I have been postponing Qt for years now, I decided to get rid of my prejudices and code a bit in C++. I named the result QStones, a Qt GUI for the algorithm discussed in my previous post, based on Suscan core library (yes, now it is also a library!) and Gqrx’s plotter widget (I have no shame, I know).
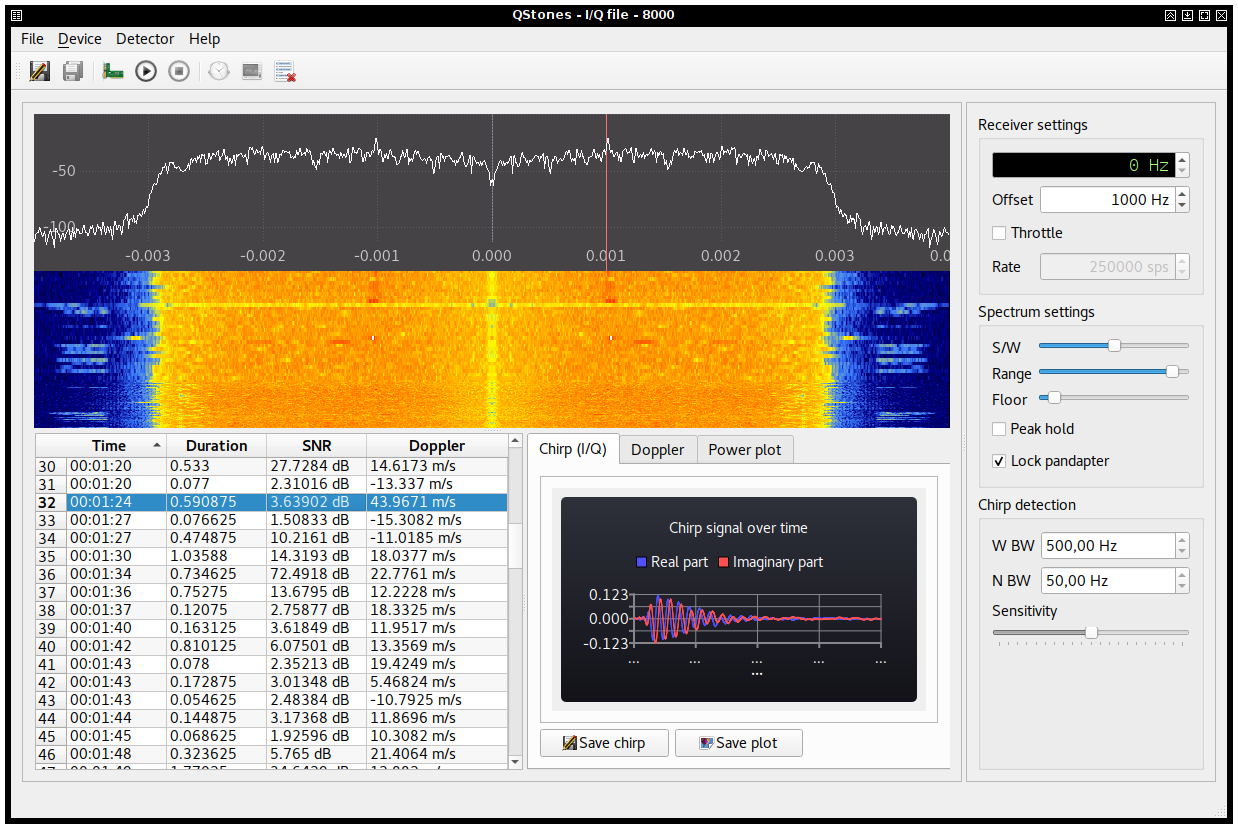
Measuring mesospheric winds with GRAVES
Last weekend I managed to plug the J-Pole antenna I built this summer to my recently acquired Yaesu FT-817 and tune it to hear GRAVES radar reflections at 143.050 MHz. But, what is GRAVES, to begin with?
GRAVES is a French space surveillance system, consisting of a bistatic radar in which the transmitting station uses 4 phased arrays covering 180º of the south of France. Each phased array scans a 45º-width sector simultaneously along with the others, with a horizontal beamwidth of 7.5º and discrete angle steps (6 in total). A full scan cycle takes 19.2 seconds before restarting again.

Demodulating NTSC for fun and profit (IV)
In the previous post we managed to frequency-demodulate the video signal, putting the black level around 0. However, we concluded that since the baseband signal amplitude was unknown, it was impossible to universally map the luminance component to the right gray level: factors like signal bandwidth, sample rate or simply the baseband gain of the transmitter’s FM modulator will strongly affect the white and sync pulse level.
Before getting to the synchronization stage, we need to stabilize the signal amplitude in order to unambiguosly map each signal level to a given gray level. This operation is performed by the AGC block.
More...Playing with one instruction set computers
After a fruitful conversation with SkUaTeR few weekeds ago, I discovered the wonderful world of OISCs (One Instruction Set Computers).
OISCs refer to (usually virtual) machines whose instruction set architecture is composed by only one instruction. The cool feature about these machines is that they are Turing complete, and therefore can be programmed to become a universal computer.
The single-instruction architecture we discussed was based on the RSSB instruction and follows a Von Neumann architecture (this is, data and code belong to the same address space).
More...Demodulating NTSC for fun and profit (III)
We refer with the generic name of “quadrature demodulators” to those demodulators that take a complex I/Q signal as input. Although this is a critical step of the demodulation process, it may also be the simplest to implement.
Let’s start by giving a look to the mathematical expression that summarizes the transmitted signal of an ideal FM modulator. If \(x(t)\) is the baseband signal, the transmitted signal \(y(t)\) will look like this:
\[y(t)=\text{cos}\left[2\pi f_ct+\pi\Delta f\int_0^tx(\tau)d\tau\right]\]With \(f_c\) being the carrier frequency. Assuming that the baseband signal’s range is \([-1, 1]\), \(\Delta f\) corresponds to the maximum bandwidth of the transmitted signal. It is clear that if \(x(t)\) is constant then \(y(t)\) is just a cosine of fixed frequency. If not, the instantaneous value of \(x(t)\) is treated as the amount of radians per unit of time (i.e. frequency) that should be added or subtracted from the carrier phase. If \(x(t)\) becomes negative, the resulting cosine has an instantaneous frequency lesser than \(f_c\). If positive, the resulting instantaneous frequency is greater than \(f_c\).
If we want to recover \(x(t)\) from \(y(t)\), then we need to undo two things: the cosine and the integral.
More...